Интегриран изпит след 7 клас? (задачи за упражнение)

"Средната оценка на изпита по математика за 6. клас, проведен на 3.10.2025, е среден 3.42.“ Според МОН шестокласниците показват добри резултати в задачи за извличане и тълкуване на данни от диаграми, но срещат трудности при работа с проценти, обикновени и десетични дроби, при прилагане на формули и изчисляване на лица на фигури.

Да проверим докъде сме стигнали... На вашето внимание няколко задачки–закачки. Опитайте първо сами, а после погледнете примерните решения.

Приятно забавление!

1. Задача: Бързо или икономично?

В туристическа хижа ученици от 7 клас приготвят супа по обща рецепта:
– Група А ползва  за 1 h котлон свързан със соларен панел, който при слънчево време има мощност 800 W.

– Група Б използва котлон включен към електрическата мрежа, който консумира мощност 1600 W и готвенето е продължило 30 min.

а) Колко kWh електроенергия използва всяка група за приготвяне на супата?

б) Ако 1 kWh струва 25 стотинки, каква е цената на използваната енергия за всяка група?

в) Коя група е по-икономична по отношение на електроенергията? Обяснете.

Решение:

Група A – соларен котлон: P₁= 800 W= 0.8 kW, време t₁ = 1 h

Група B – електрически котлон: P₂=1600 W=1.6 kW, време t₂​= 30 min = 0.5 h

Цена на 1 kWh: 25 ст = 0.25 лв

а) Енергия, изразходвана от всяка група: Използваме, че E=P×t

За група A: E₁​= 0.8×1=0.8kWh

За група B: E2= 1.6×0.5=0.8 kWh

И двете групи използват еднаква количество 0.8 kWh електроенергия.

б) Цена за електроенергия

За група A: C1=0.0 лв

За група B: C2=0.8×0.25=0.20 лв

в) Коя група е по-икономична?

Група А (соларният котлон) е по-икономична в реални условия,
защото тя използва слънчева енергия, която е безплатна — не се плаща за нея.

Двете групи изразходват еднакво количество енергия (0.8 kWh), но соларният котлон е по-икономичен и екологичен.

Извод: Макар и по-бавен, соларният котлон спестява разходи и не замърсява околната среда.

2. Задача: Газирано чудо

За училищния празник учениците решават да направят домашна газирана лимонада, като смесват сода, лимонов сок и вода. От лабораторни измервания се знае, че 5 g сода се неутрализират напълно от 25 ml лимонов сок.
Учениците планират да използват 150 g сода, а лимоновият сок се продава в бутилки от 250 ml.

а) Колко милилитра лимонов сок са необходими за неутрализирането на 150 g сода?
б) Колко бутилки лимонов сок трябва да купят?

в) Ако добавят 2 литра вода, какво общо количество лимонада ще получат?

Решение:

а) За неутрализиране на 30 пъти по-голямо количество сода (150 : 5 = 30) ще са нужни  съответно 25 . 30 = 750 ml лимонов сок.

б) Трябва да се купят съответно  750 : 250 = 3 бутилки

в) Общото количество лимонада ще бъде: Знаем, че 2 l вода = 2000 ml. 

Тогава 2000 ml вода +750 ml сок = 2750 ml =2,75 l лимонада

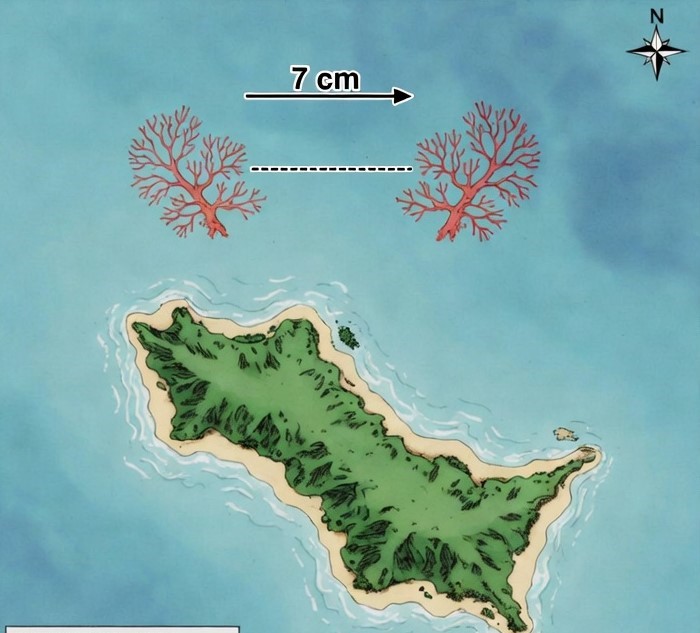
3. Задача: Коралов остров

Карта на малък остров показва, че разстоянието между два коралови рифа е 7 cm. Мащабът на картата е 1 : 100 000.

а) Намерете действителното разстояние между рифовете.

б) На острова живеят 12 000 души, а площта му е 30 km². Изчислете средната гъстота на населението.

в) Запишете две човешки дейности, които увеличават риска от избелване на коралите. Коралите са оцветени естествено в нюансите на червено, розово и оранжево.

 

Решение:

Разстояние на картата: 7 cm, мащаб 1:100 000 

а) Действително разстояние: 7.100 000 cm = 700 000 cm = 7 km

б) Гъстота на населението: 12 000: 30= 400 души/km²

в) Кои човешки дейности според вас увеличават риска от избелване на коралите?

Замърсяване с пластмаси и химикали. Повишаване на температурата на водата чрез емисии на парникови газове.

4. Задача: Кой ще победи?

Двама ученици се състезават по път с дължина 600 m. Мария се движи със скорост 2,5 m/s. Иван се движи със скорост 3 m/s, но тръгва 20 s по-късно.

а) За колко време Мария ще измине разстоянието?

б) Колко време след старта си Иван ще настигне Мария?

в) Кой ще стигне първи до финала?

г) Изразете резултатите в минути и секунди.

 Решение:

а) За колко време Мария ще измине разстоянието?

t = s : v или  600 m : 2,5 m/s ​= 240 s

Мария изминава разстоянието за 240 s = 4 min.

б) Колко време след старта си Иван ще настигне Мария?

До срещата Мария и Иван изминават едно и също разстояние, но за различно време. Мария се движи време t, а Иван се движи с 20 s по–малко,  (t –20).

Мария изминава s ₁ = 2,5 t, а Иван изминава s ₂ = s ₁ или  приравняваме двете разстояния s ₂ = 3 (t –20) = 2,5 t = s ₁

Разкриваме скобите и решаваме това просто уравнение с едно неизвестно. Получаваме времето до срещата, когато Иван настига Мария е t = 120 s.

Иван настигa Мария 100 s след своя старт, или 120 s след началото на състезанието (тъй като тръгва 20 s по-късно).

в) Кой ще стигне първи до финала?

Мария стига до финала за 240 s = 4 min.

Времето на Иван до финала е t = s : v или  600 m : 3 m/s ​= 200 s

Но той стартира 20 s по-късно, затова достига финала след 200+20 = 220 s .

Иван пристига първи.

г) Изразете резултатите в минути и секунди:

Време на Мария: 240 s = 4 min 0 s

Време на Иван: 220 s = 3 min 40 s

Иван настигa Мария след 120 s от своя старт (или 2 min 0 s от началото на състезанието) и финишира пръв — с 20 s по-рано от нея.

5. Задача: Плътност на метално кубче

Кубче от неизвестен метал има дължина на ръба 4 cm и маса 1,28 kg. Намерете обема на кубчето (в cm³ и m³). Изчислете плътността (в kg/m³) на металното кубче. Защо е важно да знаем плътността? (напишете кратко мнение)

 

Решение:

а) Кубът има обем: V=a³ V=4³=64 cm³  

За да го изразим в кубични метри:

1 cm³ =10⁻6 m³  или  1 m³ = 1 000 000 cm³

Обемът е 64 cm³ или 0,000064 m³.

б) Формула: ρ = m/V

Ρ = 1,28 kg : 000064 m³ = 20 000 kg/m³

Плътността е 20 000 kg/m³.

в) Според данните за плътността в таблицата, определете кой метал съответства приблизително на тази плътност.

Метал	Плътност (kg/m³)
Алуминий	2700
Мед	8900
Желязо	7800
Волфрам	19 300
Платина	21 450

Извод: Металът вероятно е волфрам или платина, тъй като е много по-плътен от алуминий, мед и желязо.

г) Позволява определяне вида на веществата. Помага при проектиране на машини, конструкции и плавателни съдове. Използва се за изчисляване на маса, обем и концентрация в практиката.

6. Задача: Движение и пропорции

Влак потегля от гара в 8:00 ч. и се движи със средна скорост 72 km/h.
След 45 мин той спира за 15 мин почивка, след което продължава със скорост 60 km/h. 

а) Колко километра изминава до 10:30 ч.?

б) Колко време е в движение спрямо времето на почивка (изрази като отношение)?

Решение:

а) Време за движение на влака:

От 8:00 до 9:00 се движи 45 min = ¾ h = 0,75 h  (с 15 min почивка)

От 9:00 до 10:30 се движи 90 min = 1,5 h

б) Изминато общо разстояние: s = s1 + s2 = 144 km

s1 = 0,75 h. 72 km/h = 54 km

s2 = 1,5 h. 60 km/h = 90 km

Влакът е изминал 144 km до 10:30 ч.

в) Времето в движение е 0,75 h  + 1,5 h = 2,25 h = 135 min. Времето за почивка е 15 min. Като отношение 135/15 = 9/1 или времето в движение е 9 пъти повече от времето на почивка (отношение 9:1).

7. задача: Енергия и проценти

Електрическа печка с мощност 1,8 kW работи 2 ч на ден в продължение на 30 дни. Енергийното дружество таксува 0,25 лв/ kWh.

а) Колко киловатчаса електроенергия изразходва печката общо за посоченото време?

б) Колко лева струва това?

в) Ако печката  се замени с уред, който е с 20 % по-икономичен, колко ще бъде новата месечна сметка?

Решение:

а) Употребена енергия Е = Р.t = 1,8 kW. 2h. 30 дни = 108 kWh

б) Цената на електроенергията 108 kWh . 0,25 лв/ kWh = 27 лв

в) Друг уред с мощност с 20 % по– малка или 80% от 1,8 kW

1,8 kW. 0.8 = 1,44 kW

г) Новата месечна употребена енергия Е = Р.t = 1,44 kW. 2h . 30 дни= 86,4 kWh. Новата сметка 86,4 kWh . 0,25 лв/ kWh = 21,6 лв.

За по– лесно сметката също ще бъде 80% от 27 лв или 27 лв . 0,8 = 21,6 лв.

Задача 8. Пътешествие до Луната и обратно

Космически апарат с 4 астронавти излита към Луната, която е на разстояние приблизително 384 000 km, като се движи равномерно със скорост 32 000 km/ден.

а) Колко дни ще продължи полетът до Луната и обратно до Земята?

б) Екипажът престоява на лунната повърхност 5 дни. Ако екипажът консумира по 2,5 l вода на човек дневно, колко литра вода са необходими за цялото пътешествие?

в) Какви разлики може да откриете между реалните условия на пътешествието и условията описани в задачата? Посочете няколко от тях.

Решение:

а) Време за полет до Луната и обратно

Един път (до Луната): 384 000 km : 32 000 km/ден = 12 дни.

Обратно (връщане): също 12 дни.

Общо (идване + връщане): 12+12 =24 дни.

б) Количество вода за целия полет (включително престоя)

Обща продължителност на мисията: полет до Луната 12 дни. + 5 дни престой  + полет обратно 12 дни = 29 дни.

Потребление на екипажа на ден = 4×2.5 l = 10 l/ден.

Общо необходимо количество вода = 10 l/ден×29 дни = 290 l.

в) Реалното движение на космическия кораб не е равномерно и неговата траектория не е права линия. Корабът ще измине много по–голямо разстояние при различни маневри за отиване и вращане. Астронавтите употребят много повече вода на ден за пиене, хигиена и охлаждане. Това се постига чрез рециклиране на водата изведена в космоса. Водата всъщност е в по–малко количество от 290 литра.  Под думата ден трябва да се разбира думата денонощие.