Олимпиада по физика, Областен кръг, 2011 година - 7 клас (задачи и решения)

Олимпиада по Физика, Областен кръг, 19 март 2011 година

Тема - 7 клас

Условията на задачите от 2009, 2010 и 2011 година  и техните решения можете да видите и ТУК

Решение на задача 1:

а) Изменена схема на вариант на първото свързване и след това се намира R₁:

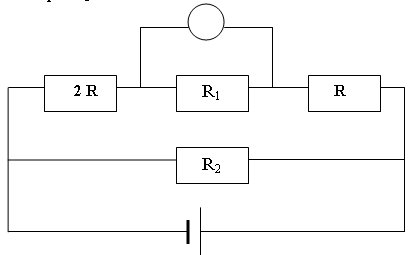
Означавам  R₃ = R, R₄ = 2R

 През R₁,  R₃, и R₄ тече ток с еднаква големина т.е. I₁ = I₃ =I₄ = I_1,3,4

 I₁ = U₁/ R₁ = U /2R₁

 Общото съпротивлене на последователно свързаните съпротивления R₁,  R₃, и R₄ е:

 R_1,3,4 = R₁ +  R₃ + R₄  = 3R + R₁

 Тогава   I_1,3,4  = U / R_1,3,4  = U / 3R + R₁

 Приравняваме:  I₁ = I_1,3,4      или  U /2R₁ = U / 3R + R₁

 Следва U.(2R₁) = U. (3R + R₁), преработваме и получаваме:

 R₁ = 3R

 б) Съгласно условието обръщам схемата за втория вид свързване съгласно условието, изпълнявам същите стъпки и се получава:

R₂ = R

Решение на  задача 2 :

1. Схеми на описаните вериги:

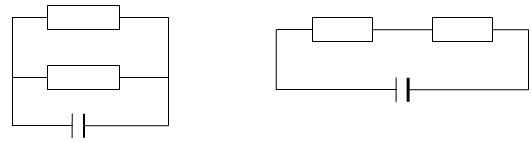
 2. При успоредно свързване консуматорите ползват еднакво напрежение U.

От техните мощности:  Р₁ = U²/R₁ и Р₂ = U²/R₂,  изразяваме

техните съпротивления:   R₁ = U²/P₁ и R₂ = U²/P₂

За последователно свързване еквивалентното съпротивление на веригата е:

R = R₁ + R₂   = U²/P₁ + U²/P₂ = U²(P₁+ P₂ / P₁P₁)

Намираме общия ток, който тече през двата консуматора при последователно свързване:       I = U / R = P₁P₂ / U (P₁+ P₂)

Тогава окончателно изразяваме:

P'₁ = I² R₁ = …= P₁P²₂ / (P₁+P₂)²

P'₂= I² R₂ = …= P²₁P₂ / (P₁+P₂)²

3. По условие  Р₁ = 50 W  и  Р₂ = 75 W за P'₁  и P'₂ получаваме съответно:

P'₁= 18 W

P'₂ = 12 W