- Новини
- Входно ниво
- 4 клас
- 5 клас
- 6 клас
- 7 клас
- 8 клас (9 ЕП клас)
- 9 клас (10 ЕП клас)
- 10 клас (11 ЕП клас)
- 11 клас (12 ЕП клас)
- Изходно ниво
- HBO за 7 клас
- Матура по Физика
- Олимпиада по Физика
- Състезания по физика и астрономия
- Човекът и природата
- Астрономия
- Физика
- Физика с усмивка
- Само факти
- Велики физици
- Нобелова награда по Физика
- За мен
Задачи по механика с решения (1 част)

1. задача
Спряла на светофар лека кола започва да се движи с постоянно ускорение 2 m/s2. В същия момент камион, който се движи с постоянна скорост от 11 m/s, изпреварва колата. На какво разстояние след светофара колата ще настигне камиона? За колко време това ще се случи?
Дадено: Търси се:
vo = 0 s =?
a = 2 m/s2 t =?
v = 11 m/s
Решение:
Двете превозни средства (кола и камион) след светофара за еднакво време t изминават едно и също разстояние s. Камионът се движи равномерно, а колата равноускорително без начална скорост.
Това ни дава право да запишем следното:
s = v . t (пътя на камиона) и s = a . t2/2 (пътя на колата)
v t = a . t2/2
(заместваме и съкращаваме)
t = 11 s
(времето, за което колата ще настигне камиона)
s = v . t = 11.11 = 121 m
(пътя изминат от превозните средства до срещата)
2. задача
Да приемем, че космическият кораб е на орбита с височина h около 280 km над повърхността на Земята и че земния радиус R е 6340 km. Ако средната скорост на космически кораб е 32 000 km / h, колко време е необходимо за една обиколка на Земята.
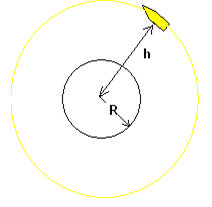
Дадено: h = 280 km, R = 6340 km, v = 32 000 km / h Търси се: t = ?
Решение:
Корабът се движи приблизително по кръгова орбита, чийто радиус е:
r = R + h = 6340 + 280 = 6620 km
s = 2π R = 6,28. 6620 = 41 573,6 km
t = s / v = 41 573,6 km / 32 000 km/h = 1,299 = 1,3 h
3.задача
В определен момент, превозното средство А е на 10 km, западно от кръстовището, а превозното средство B е 12 km, източно от същото кръстовище. Превознитте средства се движат към кръстовището с постоянна скорост, съответно А със скорост 25 km/h, а B със скорост 40 km/h. Какво ще бъде разстоянието между кръстовището и мястото на срещата на превозните средства?
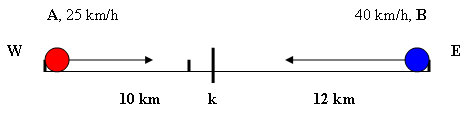
Решение:
Времето t за движение на превозните средства до мястото на срещата е еднакво, за което те ще изминат различни пътища s1 и s2. Това ни дава основание да запишем:
t = s1 / v1 = s2/ v2
Съставяме система от 2 уравнения:
s1. v2 = s2.v1
s1 + s2 = 22 km
От второто уравнение изключваме s1 = 22 - s2, заместваме във първото. Заместваме с числените стойности и получаваме:
(22 - s2 ). v2 = s2.v1
880 = 65 s2
s2= 13,5 km, s1 = 8,5 km
Търсеното разстояние е: s = 10 – 8,5 = 1,5 km, западно от кръстовището.
4. задача
Една дама бута с хоризонтална сила 8 N детска количка, чиято маса е 10 kg.
(1) Какво разстояние ще измине количката за 5s, ако тръгва от състояние на покой.
(2) Какво разстояние ще измине количката за 5 s, ако жената е поставила в нея своето бебе, което тежи 3 kg, преди да започне бутането?
Решение:
(1). Използваме F = ma, за да намерите ускорение a на количката.
8 = 10 . a a = 0,8 m/s2
Изминатото разстояние е:
s = 0 + ½. 0,8 . 52 = 10 m
(2). При втората ситуация общата маса (количка + бебе) е:
m = 10 + 3 = 13 кг
Намираме ускорението a отново чрез ІІ принцип на механиката:
F = ma, 8 = 13 .a
a = 8 / 13 = 0,62 m/s2
Изминатото разстояние е:
s = 0 + ½. 0,62 .52 = 7.8 m
5. задача
Куршум е изстрелян от пушка и напуска нейното дуло със скорост 400 m/s. Колко нютона е силата, действала върху куршума по време на пътуването през цевта, която е дълга 0,8 m. Приемаме, че масата на куршума е 5 g и че действащата сила е постоянна.
Решение:
Начална скорост на куршума vо = 0, движението е равноускорително.
От уравнението s = (v2 – v2о )/2a, а = v2/2s
намираме ускорението на куршума:
а = (4002)/2.0,8 = 100 000 m/s2
Накрая използваме ІІ принцип на Нютон за куршума:
F = m. а = 0,005 kg . 100 000 m/s2 = 500 N
Сила действаща на куршума, докато е в цевта има големина 500 N.
- Log in to post comments
- 32907 reads
